Refactoring exception handling using a free monad

Posted on January 8, 2018

Overview

In my previous post I showed how I was managing exceptions by using a “wrapper” around a record of functions. In this post I’ll show how a free monad approach can be used to achieve the same goal and compare the two techniques.

Recap

Requirements

This is the requirement for the example app, which is a pipeline of jobs

  1. Job
    1. Can run any IO action and as a result these actions can fail with exceptions
    2. This is custom code and can fail for any number of reasons, network errors, disk permissions etc
  2. Pipeline
    1. Must run impure jobs but be as pure as possible itself
    2. Must be able to handle job failure (exceptions)
    3. Supports different storage mechanisms, e.g. on disk for local dev vs cloud for production
  3. Both jobs and the pipeline should be testable

Intent

The idea was to have a record of operations, different implementations of this record are possible (e.g. run locally vs run in cloud). Then a function is called to create a wrapper function for each record field and a wrapper record is created. The functions in the wrapper record catch all synchronous exceptions and convert them to ExceptT.

The benefit of this approach was that more of the code could be written with pure functions without losing the ability to deal with exceptions that could occur at any point if the operations were specialized to IO.

data Operations m = Operations { opRead :: m Text
                               , opWrite :: Text -> m ()
                               }

data OperationsWrapper m = OperationsWrapper { opRead :: ExceptT OpsError m Text
                                             , opWrite :: Text -> ExceptT OpsError m ()
                                             }
                                             
mkOpsWrapper :: (MonadCatch m) => I2.Operations m -> OperationsWrapper m
mkOpsWrapper o = OperationsWrapper { opRead = E.ExceptT ((Right <$> I2.opRead o) `catch` readError)
                                   , ...
                                   }
  where
    readError :: (Monad m) => SomeException -> m (Either OpsError b)
    readError e = pure . Left . ErrRead $ "Error reading: " <> show e
      
    ...

Observations

Here is roughly how it worked

A quick overview of free monads

There are many great articles on what free monads are and how they are implemented, see the links below for some of them. So I wont be going into detail about how they work, rather I’ll show how they can be used. But even if you’ve never used a free monad before, you may well be able to follow along with how I use them here.

What are they?

A free monad way to build a monad from any functor. The rest of the article demonstrates why you might want to use them.

How will this help?

With a free monad you have a function that builds the free monad structure and one or more functions that interpret/run the AST.

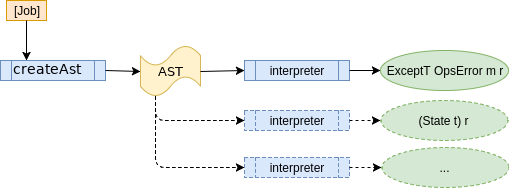
As the image above illustrates createAst generates the AST. The AST can then be passed to different interpreters that run the AST. With the record based approach you varied the implementation by choosing which record of functions to pass in. Here you use a different interpreter over the same free monad output to vary the implementation. This results in a clean separation of concerns.

Note that you don’t need to use free monads to implement this pattern. You could create an AST using sum types and have interpreters that run that. The advantage of using free is that since it is monadic you get to use Haskell’s do notation. This makes the code that generates the AST feel “natural”, it is a simple embedded domain specific language

The free operations

{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE TemplateHaskell #-}
{-# LANGUAGE DeriveFunctor #-}

module Main where

import           Control.Monad.Free
import           Control.Monad.Free.TH

data OpsF m next = OpRead (Text -> next)
                 | OpWrite Text next
                 | OpLog Text next
                 | OpRun Text (Text -> m Text) Text (Text -> next)
                 deriving (Functor)

makeFree ''OpsF
type Ops m = Free (OpsF m)

I’m using template haskell and DeriveFunctor to do all the heavy lifting. I.e. it creates all the types that lift your operations into the Free monad. Not having to manually do this makes creating free monads pretty simple. If you have not used free before I’d suggest reading some of the articles I’ve linked to below to understand the detail, or you can just follow this pattern for now

  1. The last type in the data constructor is the “return type”
  2. next is what enables the chaining
  3. If the last type is a function returning next, that means that you can bind the value

E.g. for OpWrite

-- data OpsF m next = OpWrite Text next
--                  | ...
do
  opWrite "param1"
  opWrite "param2"
  1. opWrite is the function created by template Haskell that constructs a OpWrite.
  2. opWrite takes a single param, the Text from “OpWrite Text next”
  3. Since there is a next you can have multiple statements in the do block

E.g. for OpRead

-- data OpsF m next = OpRead (Text -> next)
--                  | ...
do
  r <- opRead
  1. opRead is the function created by template Haskell that constructs a OpRead.
  2. opRead takes no parameters
  3. We can bind to the Text result the (Text -> next) from “OpRead (Text -> next)”

And here is an example using several of the DSL operations together

createAst :: (Monad m) => Text -> (Ops m) Text
createAst x = do
  opLog $ "starting: " <> x
  r <- opRead
  opWrite $ r <> x

Interpreting

After running the createAst function what you have is an AST. opRead etc do nothing on their own. This is the magic of using free with do notation. We go to write normal, pure, code and we end up with an AST.

Given this AST it is possible to write different interpreters that act in various ways. E.g. one for testing, one for local, one for running in the cloud etc.

Was this not about exceptions?

Yes, lets write an interpreter that, similar to the record wrapper approach, catches exceptions.

However before starting its worth reiterating a few points about exceptions from my previous post. Remember that it is usually a very bad idea to catch all exceptions as you may end up catching exceptions that you ought not to catch. See Exceptions best practices in Haskell for a good overview. There are several ways to ensure that you are only catch asynchronous exceptions. In these examples I’m going to be using the safe exceptions package which does exactly that.

Right, back to the code. In this example interpreterFile is a function that interprets the AST and uses a file to store/load the state

-- Make sure that the SafeException functions are used
import Protolude hiding (catch, throwIO)
import Control.Exception.Safe (catch, throwIO)


interpreterFile :: (Ops IO) Text -> ExceptT OpsError IO Text
interpreterFile o =
  case o of
    Pure a -> pure a   -- no next action

    (Free (OpRead n)) ->
      do
        r <- liftIO $ Txt.readFile "data.txt"
        interpreterFile $ n r  -- run next
      `catch`
        handler ErrRead

    (Free (OpWrite t n)) ->
      do
        liftIO $ Txt.writeFile "data.txt" t
        interpreterFile n  -- run next
      `catch`
        handler ErrWrite
      
    (Free (OpRun name fn t n)) ->
      do
        r <- lift $ fn t
        interpreterFile $ n r  -- run next
      `catch`
        handler (ErrRunning name)
      
    (Free (OpLog t n)) -> do
      putText $ "log: " <> t
      interpreterFile n  -- run next

  where
    handler :: (Monad m) => (Text -> OpsError) -> SomeException -> ExceptT OpsError m Text
    handler ope e = throwE . ope $ show e  -- catch exception and use ExceptT's throwE

The operations are run and any synchronous exception is caught and handled in the ExceptT. This looks pretty similar to the record based approach but I think is simpler.

Testing

Here is an interpreter for testing which uses a state monad to store/retrieve the state

data TestState = TestState { tstValue :: Text
                           , tstLog :: [Text]
                           } deriving (Show, Eq)

interpreterState :: (Ops (S.State TestState)) Text -> (S.State TestState) Text
interpreterState o =
  case o of
    Pure a -> do
      modify (\s -> s { tstValue = a })
      tstValue <$> get

    (Free (OpRead n)) -> do
      st <- S.get 
      interpreterState $ n (tstValue st)

    (Free (OpWrite t n)) -> do
      S.modify (\s -> s { tstValue = t } )
      interpreterState n
      
    (Free (OpRun _ fn t n)) -> do
      r <- fn t
      interpreterState $ n r
      
    (Free (OpLog t n)) -> do
      S.modify (\(TestState s ls) -> TestState s $ ls <> [t])
      interpreterState n

Compare that to the previous approach’s tests

testPipeline :: [I2.Job (S.State Text)] -> Text -> S.State Text (Either I3.OpsError Text)
testPipeline jobs initial = do
  let ops = I3.OperationsWrapper { I3.opRead = E.ExceptT $ do
                                     r <- get
                                     pure . Right $ r

The big advantage here is that the tests are no longer forced to use ExceptT. Each interpreter, for testing or otherwise, can use whatever stack is appropriate

Problems

As always there are trade offs, see the Free monad considered harmful article for example. While some of these issues can be address (e.g. see church encoding below) it is worth considering alternatives.

Personally, so far, I’ve found free to be a great fit for what I need (e.g. selecting implementation not based on type), but its definitely worth deciding on a case by case basis

Church encoding

The Control.Monad.Free.Church package handles church encoding of a free monad. This can be important to do because, as it says in Control.Monad.Free.Church:

Even if the Haskell runtime optimizes some of the overhead through laziness and generational garbage collection, the asymptotic runtime is still quadratic. On the other hand, if the Church encoding is used, the tree only needs to be constructed once.

Given how easy this package makes church encoding, and how bad O(n^2) performance can be, it is almost always a good idea to do the encoding.

(I originally found getting the types correct for Church encoding a bit tricky. This Free monad and church encoding example helped clear up a lot of the confusion for me. Be sure to look at it as well if my explanation below does not help you).

To get Church encoding, the only requirement is that you use a MonadFree constraint rather than your more specific data type for the function that generates the DSL.

In the example above createAst looked like this.

createAst :: (Monad m) => Text -> (Ops m) Text
createAst x = do

The problem is that I’ve used the “Ops m” type, rather than MonadFree.

Here is what it should look like

createAst :: (Monad m, MonadFree (OpsF m) a) => Text -> [Job m] -> a Text
createAst x = do

The important parts being

createAst :: (Monad m, MonadFree (OpsF m) a) => ............... -> a Text
createAst x = do

This is how it would be run without Church encoding

  --------------------------------------------------
  -- Example in IO with exception
  --------------------------------------------------
  let ioJobs = [ Job "j1" ioJob1
               , Job "j2" ioJob2
               , Job "j3" ioJob3
               ]
  
  a <- runExceptT $ interpreterFile $ createAst "test1" ioJobs
  print a

And this is how its run with Church encoding using improve from Control.Monad.Free.Church

  --------------------------------------------------
  -- Example in IO with exception
  --------------------------------------------------
  let ioJobs = [ Job "j1" ioJob1
               , Job "j2" ioJob2
               , Job "j3" ioJob3
               ]
  
        -- Note that createAst must be run inline here to avoid an error about the monad constraints
  ai <- runExceptT $ interpreterFile (C.improve $ createAst "test1" ioJobs)
  print ai

That is all it takes, we can now use free without O(n^2) concerns

Conclusion

Free monads give us a nice way to separate pure and impure code while also handling exceptions. Overall I think this approach is more flexible and easier to read that the record of functions approach.

Links